data(penguins, package="palmerpenguins")
fit1 = lm(formula = body_mass_g ~ flipper_length_mm, data = penguins)
coefficients(fit1) (Intercept) flipper_length_mm
-5780.83136 49.68557 The idea of regression analysis is to approximate a univariate dependent variable Y_i (also known the regressand or response variable) as a function of the k-variate vector of the independent variables \boldsymbol X_i (also known as regressors or predictor variables). The relationship is formulated as Y_i \approx f(\boldsymbol X_i), \quad i=1, \ldots, n, where Y_1, \ldots, Y_n is a dataset for the dependent variable and \boldsymbol X_1, \ldots, \boldsymbol X_n a corresponding dataset for the regressor variables.
The goal of the least squares method is to find the regression function that minimizes the squared difference between actual and fitted values of Y_i: \min_{f(\cdot)} \sum_{i=1}^n (Y_i - f(\boldsymbol X_i))^2. If the regression function f(\boldsymbol X_i) is linear in \boldsymbol X_i, i.e., f(\boldsymbol X_i) = b_1 + b_2 X_{i2} + \ldots + b_k X_{ik} = \boldsymbol X_i'\boldsymbol b, \quad \boldsymbol b \in \mathbb R^k, the minimization problem is known as the ordinary least squares (OLS) problem. To avoid the unrealistic constraint of the regression line passing through the origin, a constant term (intercept) is always included in \boldsymbol X_i, typically as the first regressor: \boldsymbol X_i = (1, X_{i2}, \ldots, X_{ik})'.
Despite its linear framework, linear regressions can be quite adaptable to nonlinear relationships by incorporating nonlinear transformations of the original regressors. Examples include polynomial terms (e.g., squared, cubic), interaction terms (combining continuous and categorical variables), and logarithmic transformations.
The sum of squared errors for a given coefficient vector \boldsymbol b \in \mathbb R^k is defined as S_n(b) = \sum_{i=1}^n (Y_i - f(\boldsymbol X_i))^2 = \sum_{i=1}^n (Y_i - \boldsymbol X_i'\boldsymbol b)^2. It is minimized by the least squares coefficient vector \widehat{\boldsymbol \beta} = \argmin_{\boldsymbol b \in \mathbb R^k} \sum_{i=1}^n (Y_i - \boldsymbol X_i'\boldsymbol b)^2.
Least squares coefficients
If the k \times k matrix (\sum_{i=1}^n \boldsymbol X_i \boldsymbol X_i') is invertible, the solution for the ordinary least squares problem is uniquely determined by \widehat{\boldsymbol \beta} = \Big( \sum_{i=1}^n \boldsymbol X_i \boldsymbol X_i' \Big)^{-1} \sum_{i=1}^n \boldsymbol X_i Y_i.
The fitted values or predicted values are \widehat Y_i = \widehat \beta_1 + \widehat \beta_2 X_{i2} + \ldots + \widehat \beta_k X_{ik} = \boldsymbol X_i'\widehat{\boldsymbol \beta}, \quad i=1, \ldots, n. The residuals are the difference between observed and fitted values: \widehat u_i = Y_i - \widehat Y_i = Y_i - \boldsymbol X_i'\widehat{\boldsymbol \beta}, \quad i=1, \ldots, n.
Let’s examine the linear relationship between a penguin’s body mass and its flipper length:
data(penguins, package="palmerpenguins")
fit1 = lm(formula = body_mass_g ~ flipper_length_mm, data = penguins)
coefficients(fit1) (Intercept) flipper_length_mm
-5780.83136 49.68557 The fitted regression line is -5781 + 49.69 \ \text{flipperlength}. We can plot the regression line over a scatter plot of the data:
par(mfrow = c(1,2), cex=0.8)
plot(penguins$flipper_length_mm, penguins$body_mass_g)
abline(fit1, col="blue")
plot(fit1$model$flipper_length_mm, residuals(fit1))
abline(0,0,col="blue")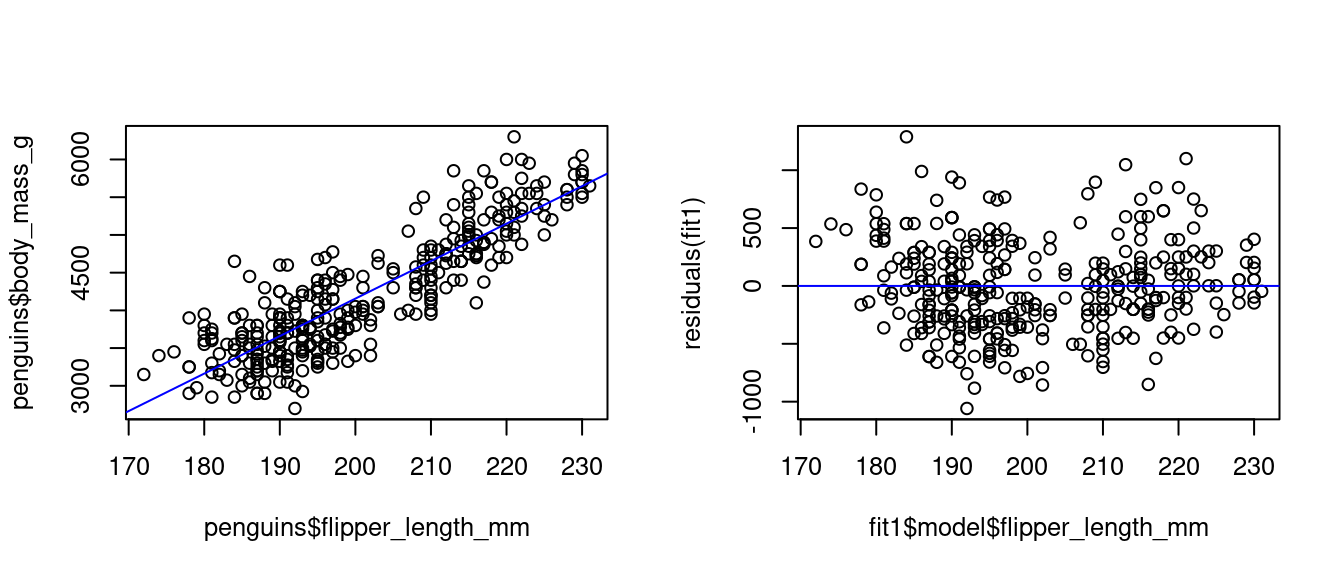
Let’s include bill depth as an additional regressor:
fit2= lm(formula = body_mass_g ~ flipper_length_mm + bill_depth_mm,
data = penguins)
coefficients(fit2) (Intercept) flipper_length_mm bill_depth_mm
-6541.90750 51.54144 22.63414 A 3D plot provides a visual representation of the resulting regression line (surface):
library(scatterplot3d) # package for 3d plots
Y = penguins$body_mass_g
X_2 = penguins$flipper_length_mm
X_3 = penguins$bill_depth_mm
plot3d <- scatterplot3d(x = penguins$flipper_length_mm,
y = penguins$bill_depth_mm,
z = penguins$body_mass_g,
angle = 60, scale.y = 0.8, pch = 16,
color ="red", xlab = "flipper_length_mm",
ylab = "bill_depth_mm",
main ="OLS Regression Surface")
plot3d$plane3d(fit2, lty.box = "solid", col=gray(.5), draw_polygon=TRUE)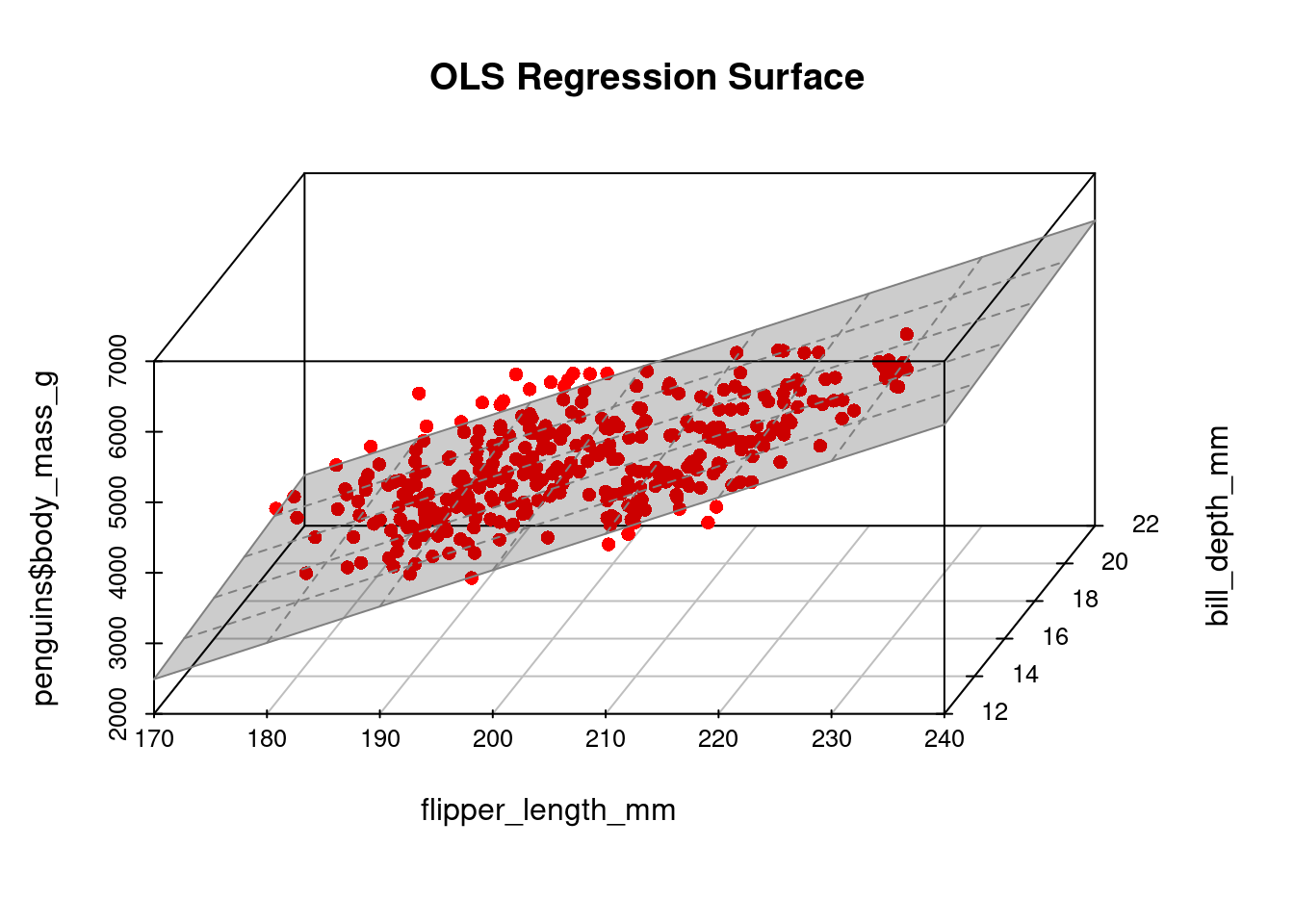
Adding the additional predictor bill length gives a model with dimensions beyond visual representation:
fit3 = lm(body_mass_g ~ flipper_length_mm + bill_depth_mm + bill_length_mm,
data = penguins)
coefficients(fit3) (Intercept) flipper_length_mm bill_depth_mm bill_length_mm
-6424.76470 50.26922 20.04953 4.16182 The fitted regression line now includes three predictors and four coefficients: -6425 + 50.27 \ \text{flipperlength} + 20.05 \ \text{billdepth} + 4.16 \ \text{billlength}
For models with multiple regressors, fitted values and residuals can still be visualized:
The pattern of fitted values arises because the observations are sorted by penguin species.
Matrix notation is convenient because it eliminates the need for summation symbols and indices. We define the response vector \boldsymbol Y and the regressor matrix (design matrix) \boldsymbol X as follows: \boldsymbol Y = \begin{pmatrix} Y_1 \\ Y_2 \\ \vdots \\ Y_n \end{pmatrix}, \quad \boldsymbol X = \begin{pmatrix} \boldsymbol X_1' \\ \boldsymbol X_2' \\ \vdots \\ \boldsymbol X_n' \end{pmatrix} = \begin{pmatrix} 1 & X_{12} & \ldots & X_{1k} \\ \vdots & & & \vdots \\ 1 & X_{n2} &\ldots & X_{nk} \end{pmatrix} Note that \sum_{i=1}^n \boldsymbol X_i \boldsymbol X_i' = \boldsymbol X'\boldsymbol X and \sum_{i=1}^n \boldsymbol X_i Y_i = \boldsymbol X' \boldsymbol Y.
The least squares coefficient vector becomes \widehat{\boldsymbol \beta} = \Big( \sum_{i=1}^n \boldsymbol X_i \boldsymbol X_i' \Big)^{-1} \sum_{i=1}^n \boldsymbol X_i Y_i = (\boldsymbol X'\boldsymbol X)^{-1} \boldsymbol X'\boldsymbol Y. The vector of fitted values can be computed as follows: \widehat{\boldsymbol Y} = \begin{pmatrix} \widehat Y_1 \\ \vdots \\ \widehat Y_n \end{pmatrix} = \boldsymbol X \widehat{\boldsymbol \beta} = \underbrace{\boldsymbol X (\boldsymbol X'\boldsymbol X)^{-1} \boldsymbol X'}_{=\boldsymbol P}\boldsymbol Y = \boldsymbol P \boldsymbol Y. The projection matrix \boldsymbol P is also known as the influence matrix or hat matrix and maps observed values to fitted values.
The vector of residuals is given by \widehat{\boldsymbol u} = \begin{pmatrix} \widehat u_1 \\ \vdots \\ \widehat u_n \end{pmatrix} = \boldsymbol Y - \widehat{\boldsymbol Y} = (\boldsymbol I_n - \boldsymbol P) \boldsymbol Y.
The diagonal entries of \boldsymbol P, given by h_{ii} = \boldsymbol X_i'(\boldsymbol X' \boldsymbol X)^{-1} \boldsymbol X_i, are called leverage values or hat values and measure how far away the regressor values of the i-th observation X_i are from those of the other observations.
Properties of leverage values: 0 \leq h_{ii} \leq 1, \quad \sum_{i=1}^n h_{ii} = k.
A large h_{ii} occurs when the observation i has a big influence on the regression line, e.g., the last observation in the following dataset:
X=c(10,20,30,40,50,60,70,500)
Y=c(1000,2200,2300,4200,4900,5500,7500,10000)
plot(X,Y, main="OLS regression line with and without last observation")
abline(lm(Y~X), col="blue")
abline(lm(Y[1:7]~X[1:7]), col="red")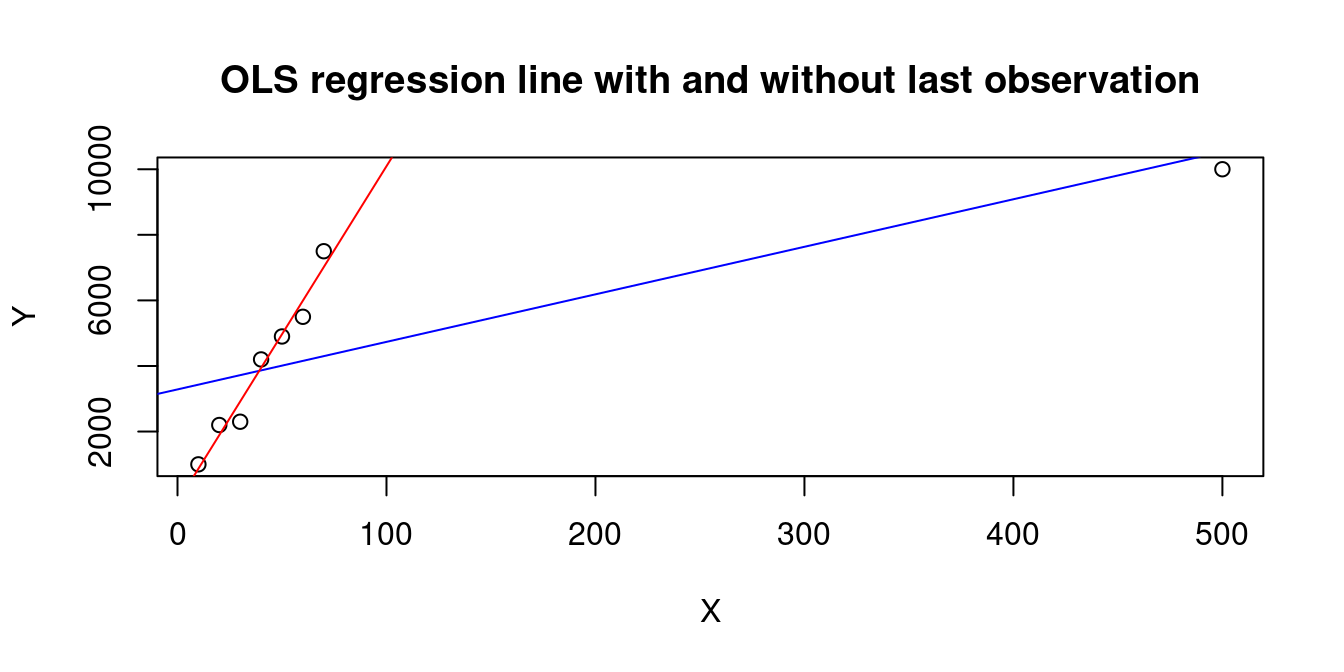
1 2 3 4 5 6 7 8
0.1657356 0.1569566 0.1492418 0.1425911 0.1370045 0.1324820 0.1290237 0.9869646 The residuals satisfy \boldsymbol X' \widehat{\boldsymbol u} = \boldsymbol 0 and \widehat{\boldsymbol Y}'\widehat{\boldsymbol u} = 0. The intercept in the regression model ensures \sum_{i=1}^n \widehat u_i = 0 and \sum_{i=1}^n \widehat Y_i = \sum_{i=1}^n Y_i.
Therefore, the sample variances have the following representations:
| Dependent variable | \widehat \sigma_Y^2 = \frac{1}{n} \sum_{i=1}^n (Y_i - \overline Y)^2 |
| Fitted values | \widehat \sigma_{\widehat Y}^2 = \frac{1}{n} \sum_{i=1}^n (\widehat Y_i - \overline{\widehat Y})^2 |
| Residuals | \widehat \sigma_{\widehat u}^2 = \frac{1}{n} \sum_{i=1}^n \widehat u_i^2 |
| Analysis of variance formula | \widehat \sigma_Y^2 = \widehat \sigma_{\widehat Y}^2 + \widehat \sigma_{\widehat u}^2 |
The larger the proportion of the explained sample variance, the better the fit of the OLS regression. This motivates the definition of the R-squared coefficient: R^2= \frac{\sum_{i=1}^n (\widehat Y_i - \overline{\widehat Y})^2}{\sum_{i=1}^n (Y_i - \overline Y)^2} = 1 - \frac{\sum_{i=1}^n \widehat u_i^2}{\sum_{i=1}^n (Y_i - \overline Y)^2}.
The R-squared describes the proportion of sample variation in \boldsymbol Y explained by \widehat{\boldsymbol Y}. Equivalently, it can be expressed as: R^2 = \widehat \sigma_{\widehat Y}^2/\widehat \sigma_{Y}^2 or R^2 = 1 - \widehat \sigma_{\widehat u}^2/\widehat \sigma_{Y}^2. We have 0\leq R^2\leq 1.
In a regression of Y_i on a single regressor Z_i with intercept (simple linear regression), the R-squared is equal to the squared sample correlation coefficient of Y_i and Z_i.
An R-squared of 0 indicates no sample variation in \widehat{\boldsymbol{Y}} (a flat regression line/surface), whereas a value of 1 indicates no variation in \widehat{\boldsymbol{u}}, indicating a perfect fit. The higher the R-squared, the better the OLS regression fits the data.
However, a low R-squared does not necessarily mean the regression specification is bad. It just implies that there is a high share of unobserved heterogeneity in \boldsymbol Y that is not captured by the regressors \boldsymbol X linearly.
Conversely, a high R-squared does not necessarily mean a good regression specification. It just means that the regression fits the sample well. Too many unnecessary regressors lead to overfitting.
If k=n, we have R^2 = 1 even if none of the regressors has an actual influence on the dependent variable.
We lose k degrees of freedom in the OLS regression since we have k regressors (k linear restrictions). Similar to the adjusted sample variance of Y, s_Y^2 = \frac{1}{n-1}\sum_{i=1}^n (Y_i - \overline Y)^2, where we adjust for the fact that we lose 1 degree of freedom due to the sample mean (one linear restriction), the adjusted sample variance of the residuals is s_{\widehat u}^2 = \frac{1}{n-k}\sum_{i=1}^n \widehat u_i^2. By incorporating adjusted versions in the R-squared definition, we penalize regression specifications with large k. The adjusted R-squared is \overline{R}^2 = 1 - \frac{\frac{1}{n-k}\sum_{i=1}^n \widehat u_i^2}{\frac{1}{n-1}\sum_{i=1}^n (Y_i - \overline Y)^2} = 1 - \frac{s_{\widehat u}^2}{s_Y^2}.
The squareroot of the adjusted sample variance of the residuals is called the standard error of the regression (SER) or residual standard error: SER := s_{\widehat u} = \sqrt{ \frac{1}{n-k}\sum_{i=1}^n \widehat u_i^2 }.
The R-squared should be used for interpreting the share of variation explained by the fitted regression line. The adjusted R-squared should be used for comparing different OLS regression specifications.
The commands summary(fit)$r.squared and summary(fit)$adj.r.squared return the R-squared and adjusted R-squared values, respectively. The SER can be returned by summary(fit)$sigma.
The stargazer() function can be used to produce nice regression outputs:
library(stargazer)stargazer(fit1, fit2, fit3, type="html", report="vc*",
omit.stat = "f", star.cutoffs = NA, df=FALSE,
omit.table.layout = "n", digits = 4)| Dependent variable: | |||
| body_mass_g | |||
| (1) | (2) | (3) | |
| flipper_length_mm | 49.6856 | 51.5414 | 50.2692 |
| bill_depth_mm | 22.6341 | 20.0495 | |
| bill_length_mm | 4.1618 | ||
| Constant | -5,780.8310 | -6,541.9080 | -6,424.7650 |
| Observations | 342 | 342 | 342 |
| R2 | 0.7590 | 0.7610 | 0.7615 |
| Adjusted R2 | 0.7583 | 0.7596 | 0.7594 |
| Residual Std. Error | 394.2782 | 393.1784 | 393.4048 |
OLS should be considered for regression problems with k << n (small k and large n). When the number of predictors k approaches or equals the number of observations n, we run into the problem of overfitting. Specifically, at k = n, the regression line will perfectly fit the data.
par(mfrow=c(1,2))
## k=n=2
Y = c(0.7,-1.0)
X = c(1.9,0.8)
fit1 = lm(Y~X)
plot(X,Y, main="OLS with k=n=2")
abline(fit1)
## k=n=3
# Some given data
Y = c(0.7,-1.0,-0.2)
X_2 = c(1.9,0.8,1.25)
X_3 = c(66, 62, 59)
fit2 = lm(Y ~ X_2 + X_3)
plot3d <- scatterplot3d(x = X_2, y = X_3, z = Y,
angle = 33, scale.y = 0.8, pch = 16,
color ="red",
xlab = "X_2",
ylab = "X_3",
main ="OLS with k=n=3")
plot3d$plane3d(fit2, lty.box = "solid", col=gray(.5), draw_polygon=TRUE)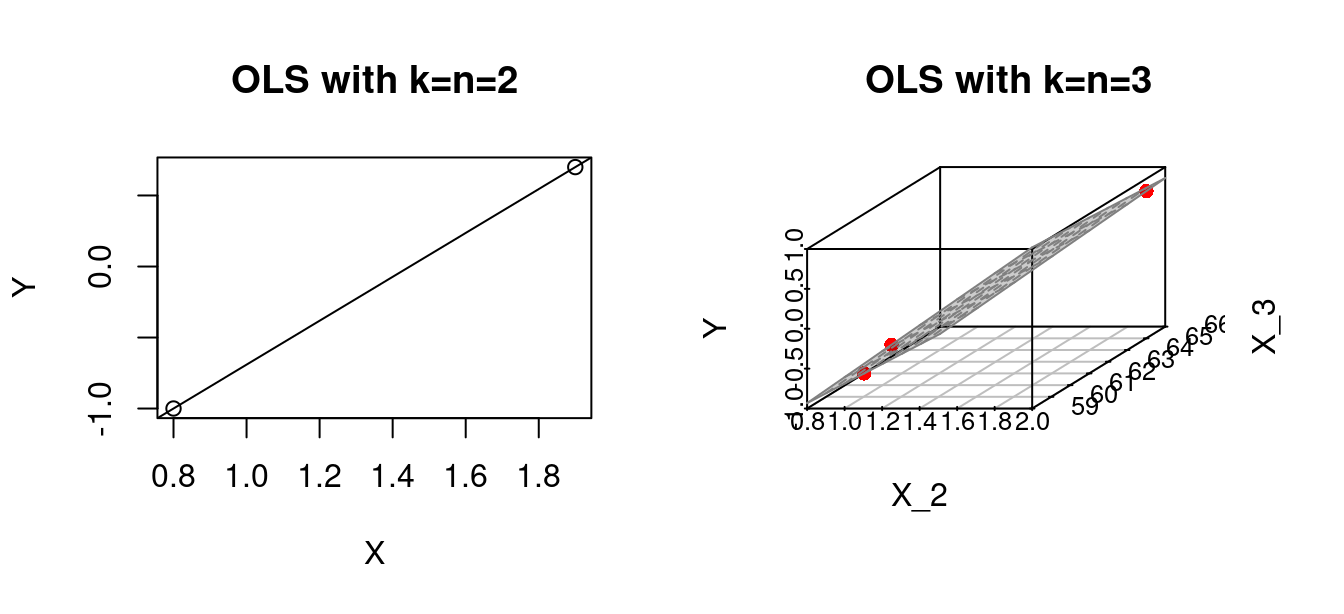
If k=n \geq 4, we can no longer visualize the OLS regression line, but the problem of a perfect fit is still present. If k > n, there exists no OLS solution because \boldsymbol X' \boldsymbol X is not invertible. Regression problems with k \approx n or k>n are called high-dimensional regressions.
The only requirement for computing the OLS coefficients is the invertibility of the matrix \boldsymbol X' \boldsymbol X. As discussed above, a necessary condition is that k \leq n.
Another reason the matrix may not be invertible is if two or more regressors are perfectly collinear. Two variables are perfectly collinear if their sample correlation is 1 or -1. Multicollinearity arises if one variable is a linear combination of the other variables.
Common causes are duplicating a regressor or using the same variable in different units (e.g., GDP in both EUR and USD).
Perfect multicollinearity (or strict multicollinearity) arises if the regressor matrix does not have full column rank: \text{rank}(\boldsymbol X) < k. It implies \text{rank}(\boldsymbol X' \boldsymbol X) < k, so that the matrix is singular and \widehat{\boldsymbol \beta} cannot be computed.
Near multicollinearity occurs when two columns of \boldsymbol X have a sample correlation very close to 1 or -1. Then, (\boldsymbol X' \boldsymbol X) is “near singular”, its eigenvalues are very small, and (\boldsymbol X' \boldsymbol X)^{-1} becomes very large, causing numerical problems.
Multicollinearity means that at least one regressor is redundant and can be dropped.
A common cause of strict multicollinearity is the inclusion of too many dummy variables. Let’s add a dummy for each penguin species:
library(fastDummies)
penguins.new = dummy_cols(penguins,select_columns = "species")
fit4 = lm(body_mass_g ~ flipper_length_mm + species_Chinstrap
+ species_Gentoo + species_Adelie, data=penguins.new)
coefficients(fit4) (Intercept) flipper_length_mm species_Chinstrap species_Gentoo
-4031.4769 40.7054 -206.5101 266.8096
species_Adelie
NA Here, the dummy variables for penguin species are collinear with the intercept variable because D_{chinstrap} + D_{gentoo} + D_{adelie} = 1, leading to a singular matrix \boldsymbol X' \boldsymbol X. The dummy variable D_{adelie} is redundant because its value can always be recovered from D_{gentoo} and D_{chinstrap}.
The solution is to use one dummy variable less than factor levels, as R automatically does by omitting the last dummy variable. Note that the coefficient for species Adelie is NA.
Alternatively, we can incorporate the factor variable species directly in the regression formula as lm() automatically generates the correct amount of dummy variables:
fit5 = lm(body_mass_g ~ flipper_length_mm + species, data=penguins)
coefficients(fit5) (Intercept) flipper_length_mm speciesChinstrap speciesGentoo
-4031.4769 40.7054 -206.5101 266.8096